(I would strongly encourage you to try to find a win for white before reading)
Modern day computers may be able to perform quadrillions of operations a second with unerring accuracy and total precision, but you can lean back with your hands on your hips and laugh in their expressionless faces. They are little more than assemblies of metal and plastic with the odd sprinkling of exotic materials and deep down, they know it.
You, on the other hand, are an organic calculating marvel unrestrained by not having to simplify everything to ones and noughts to make sense of anything, with an insight honed over many thousands of years with that most prized human ability, creativity, that machines could only dream of had they processed that basic capability. You perform complex calculations combining Newton’s Laws of motion with advanced Euclidean geometry every time you cross the road to avoid collision, barely noticing such a background task. Faced with the challenge of calculating a 30+ move line of play leading to the only available win in all possible variations, there is only ever going to be one winner – YOU.
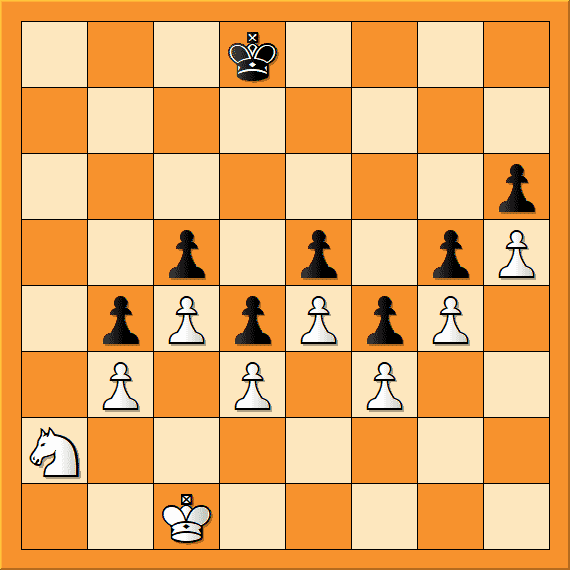Take the following endgame for example. Each player has around half-a-dozen moves available per turn which gives over forty-six thousand possible ways of playing the next three moves each. Even with modern pruning techniques, the solution quickly falls beyond any computer engine’s horizon.
You, on the other hand, would take a human approach without having to resort to such calculation and simply image where you would like to put the white King and Knight anywhere on the board. After not too long consideration, you would discover that a win would be possible by getting the knight to h4 with the king on h3. It would then normally be a case of finding a route for the knight which disappointingly proves not to be possible. During the attempt however, it can be seen that the knight can get to the other side via the a4 square.
With this new train of thought, it is easy to see that the black king can always protect its c-pawn but cannot prevent the knight from getting to d5 though this is of limited value because the black king can easily defend both the f6 and e7 squares to prevent the knight from ever attacking the h-pawn and always get back to defend the c-pawn if necessary. So if the knight goes through, it can’t do any damage on its own. Hmmm.
Okay, what if you position the white king on a2 or b2 and bring the knight back to join the king via a3? How do things look after pawn takes knight followed by king takes pawn? It becomes easily apparent that it depends on the position of the black king which will surely follow the knight back to guard against this possible invasion. Ah, but wait. When the white knight is on d5, the black king has to alternate between e6 and f7 to prevent the knight from attacking the h-pawn. If the black king is on e6, it can just keep up with the knight enough as it races back to a3 to enable pawn takes knight and keep the white king out. If however, the king is on f7, it is one move too slow. It doesn’t matter whether the white king is on a2 or b2 to assist the knight’s return so this can be used to waste a move if necessary to force the black king to f7.
If the black king is pushed to f7 and the knight races back to a3, it cannot be taken and as the black king moves within range, it can slip back to c2. After all that, the only thing that has been achieved is that the white knight is on c2 instead of a2 as in the start position. Why is that significant? Well, we can now go back to the first train of thought; the knight can now get to h4! Once supported by the king at h4, black has no option but to take it otherwise it will get to f5. After the king re-capture it is quite easy to see that it will gain entry by pushing the released g-pawn and mop up.
Finally, you can set the winning plan into action – Move the white king to the left in readiness. Bounce the knight off the h-file to enter the black camp via a4; manoeuvre the knight to d5 and use the king to push the black king to f7; return the knight to the white camp via a3; position the white knight at h3; move the knight into h4; re-take the forced capture and use the g-pawn to gain entry.
Believe it or not, although quite easy to visualise because of the very small number of mobile pieces, this sequence is over thirty moves which takes it well beyond most computer programs. So, you can quite legitimately claim that in certain positions, you are stronger than the World’s most powerful computers and when asked how far ahead you calculate, you can confidently assert that on occasions where necessary, you calculate over thirty moves ahead. You are indeed SUPERHUMAN.